CK-12 Algebra Explorations is a hands-on series of activities that guides students from Pre-K to Grade 7 through algebraic concepts.
Material Type: Activity/Lab, Teaching/Learning Strategy
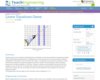
Students groups act as aerospace engineering teams competing to create linear equations to guide space shuttles safely through obstacles generated by a modeling game in level-based rounds. Each round provides a different configuration of the obstacle, which consists of two "gates." The obstacles are presented as asteroids or comets, and the linear equations as inputs into autopilot on board the shuttle. The winning group is the one that first generates the successful equations for all levels. The game is created via the programming software MATLAB, available as a free 30-day trial. The activity helps students make the connection between graphs and the real world. In this activity, they can see the path of a space shuttle modeled by a linear equation, as if they were looking from above.
Material Type: Activity/Lab
This task requires students to think about equations and solve them using pictures.
Material Type: Activity/Lab
In Module 4, students extend what they already know about unit rates and proportional relationships to linear equations and their graphs. Students understand the connections between proportional relationships, lines, and linear equations in this module. Students learn to apply the skills they acquired in Grades 6 and 7, with respect to symbolic notation and properties of equality to transcribe and solve equations in one variable and then in two variables.
Material Type: Module
This module consolidates and expands upon students understanding of equivalent expressions as they apply the properties of operations to write expressions in both standard form and in factored form. They use linear equations to solve unknown angle problems and other problems presented within context to understand that solving algebraic equations is all about the numbers. Students use the number line to understand the properties of inequality and recognize when to preserve the inequality and when to reverse the inequality when solving problems leading to inequalities. They interpret solutions within the context of problems. Students extend their sixth-grade study of geometric figures and the relationships between them as they apply their work with expressions and equations to solve problems involving area of a circle and composite area in the plane, as well as volume and surface area of right prisms.
Material Type: Module
In earlier modules, students analyze the process of solving equations and developing fluency in writing, interpreting, and translating between various forms of linear equations (Module 1) and linear and exponential functions (Module 3). These experiences combined with modeling with data (Module 2), set the stage for Module 4. Here students continue to interpret expressions, create equations, rewrite equations and functions in different but equivalent forms, and graph and interpret functions, but this time using polynomial functions, and more specifically quadratic functions, as well as square root and cube root functions.
Material Type: Module
This is a task from the Illustrative Mathematics website that is one part of a complete illustration of the standard to which it is aligned. Each task has at least one solution and some commentary that addresses important asects of the task and its potential use. Here are the first few lines of the commentary for this task: The following is a student solution to the inequality \frac{5}{18} - \frac{x-2}{9} \leq \frac{x-4}{6}. \begin{align} \frac{5}{18} - \frac{x-2}{9} & \le...
Material Type: Activity/Lab
This task does not actually require that the student solve the system but that they recognize the pairs of linear equations in two variables that would be used to solve the system. This is an important step in the process of solving systems.
Material Type: Activity/Lab
This task is the last in a series of three tasks that use inequalities in the same context at increasing complexity in 6th grade, 7th grade and in HS algebra. Students write and solve inequalities, and represent the solutions graphically. The progression of the content standards is 6.EE.8 to 7.EE.4 to A-REI.12.
Material Type: Activity/Lab
In this problem, students are given a picture of two triangles that appear to be similar, but whose similarity cannot be proven without further information. Asking students to provide a sequence of similarity transformations that maps one triangle to the other focuses them on the work of standard G-SRT.2, using the definition of similarity in terms of similarity transformations.
Material Type: Activity/Lab
This problem provides students with an opportunity to discover algebraic structure in a geometric context. More specifically, the student will need to divide up the given polygons into triangles and then use the fact that the sum of the angles in each triangle is 180_.
Material Type: Activity/Lab
This middle school geometry lesson is submitted by Andre Douglas, Secondary Mathematics Teacher in the Virgin Islands Department of Education. Mr. Douglas extends this lesson beyond geometry to help students gain an appreciation of the fish and wildlife in this US territory. Teachers using this lesson plan can extend this lesson through information provided by the National Park Service website: https://www.nps.gov/viis/learn/kidsyouth/queen_parrotfish.htm
Material Type: Homework/Assignment
Module 4 builds upon Module 2s work with place value within 20, now focusing on the role of place value in the addition and subtraction of numbers to 40. Students study, organize, and manipulate numbers within 40. They compare quantities and begin using the symbols for greater than (>) and less than (<). Addition and subtraction of tens is another focus of this module as is the use of familiar strategies to add two-digit and single-digit numbers within 40. Near the end of the module, the focus moves to new ways to represent larger quantities and adding like place value units as students add two-digit numbers.
Material Type: Module
Module 2 serves as a bridge from students' prior work with problem solving within 10 to work within 100 as students begin to solve addition and subtraction problems involving teen numbers. Students go beyond the Level 2 strategies of counting on and counting back as they learn Level 3 strategies informally called "make ten" or "take from ten."
Material Type: Module
This is an instructional task related to deepening place-value concepts. The important piece of knowledge upon which students need to draw is that 10 tens is 1 hundred.
Material Type: Activity/Lab
This task gives children an opportunity to subtract a three-digit number including a zero that requires regrouping. The solutions show how students can solve this problem before they have learned the traditional algorithm.
Material Type: Activity/Lab
In this task students are required to compare numbers that are identified by word names and not just digits. The order of the numbers described in words are intentionally placed in a different order than their base-ten counterparts so that students need to think carefully about the value of the numbers.
Material Type: Activity/Lab
This activity provides many ideas for celebrating the 100th Day of school.
Material Type: Lesson Plan
This task helps students understand the relationship between digit placement and the value of a number.
Material Type: Activity/Lab
In Module 4, students developed addition and subtraction fluency within 100 and began developing conceptual understanding of the standard algorithm via place value strategies. In Module 5, students build upon their mastery of renaming place value units and extend their work with conceptual understanding of the addition and subtraction algorithms to numbers within 1,000, always with the option of modeling with materials or drawings. Throughout the module, students continue to focus on strengthening and deepening conceptual understanding and fluency.
Material Type: Module
